Measuring the Competitiveness at Tennis Majors from 2000-2016

Introduction

After I published my previous analysis of scorelines at tennis majors, many asked for a more detailed examination. Ben Rothenberg of The New York Times, the inspiration for that analysis, tweeted: ...curious also about how often fourth or fifth sets are uncompetitive because one guy is gassed/dispirited, compared to BO3.

In response, I've taken a deeper look at the ebbs and flows of these matches. Do matches vary in competitiveness on a consistent basis? Is there evidence that the later sets of a match are more dominated by the eventual winner? Also, as a match progresses, is there any way to predict who has the advantage in winning the match? What follows may help in answering these questions and more.

The following analysis is based on all completed matches at majors from 2000-2016 less retirements and walkovers. This includes 8,253 matches that are comprised of 30,445 sets and 298,027 games. Please note that all majors, except for the U.S. Open, do not use tiebreaks in the final set. This will slightly inflate the fifth-set averages concerning games where applicable.

Global Averages


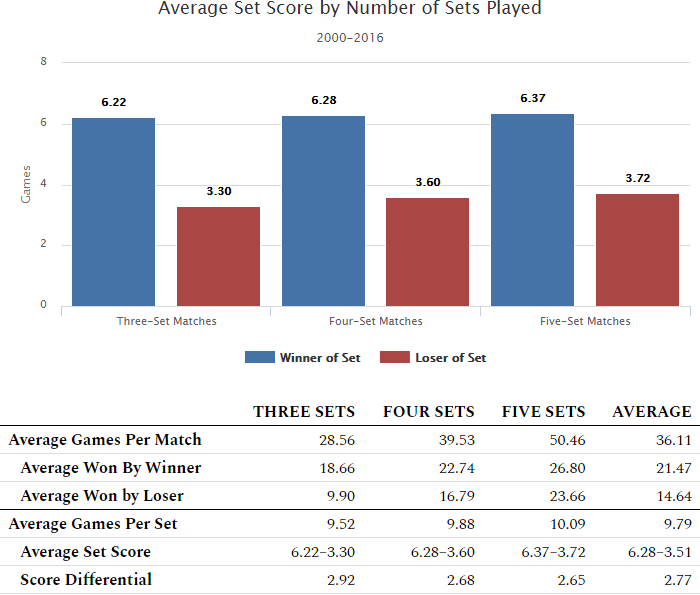
	Three Sets	Four Sets	Five Sets	Average
Average Games Per Match	28.56	39.53	50.46	36.11
Average Won By Winner	18.66	22.74	26.80	21.47
Average Won by Loser	9.90	16.79	23.66	14.64
Average Games Per Set	9.52	9.88	10.09	9.79
Average Set Score	6.22–3.30	6.28–3.60	6.37–3.72	6.28–3.51
Score Differential	2.92	2.68	2.65	2.77

Note:

The Average Set Score does not differentiate between who ultimately won or lost the match; it is a measure of the overall competitiveness of an average set.
Using the Score Differential as the criterion, there is a greater disparity in competitiveness between three-set and four-set matches than there is between four-set and five-set matches.

Three-Set Matches


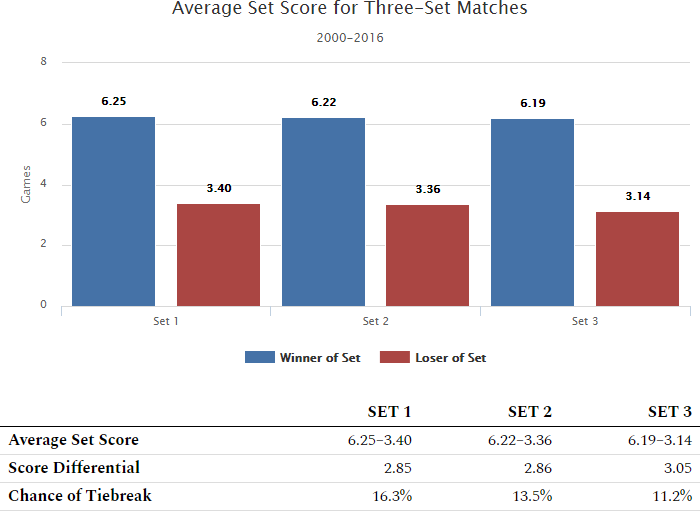
	Set 1	Set 2	Set 3
Average Set Score	6.25–3.40	6.22–3.36	6.19–3.14
Score Differential	2.85	2.86	3.05
Chance of Tiebreak	16.3%	13.5%	11.2%

Note:

The first two sets are roughly equal in competitiveness. The third set, though, is more dominated by the winner of the match. This can be inferred by the jump in Score Differential in the third set and the continued decrease in tiebreaks.

Four-Set Matches


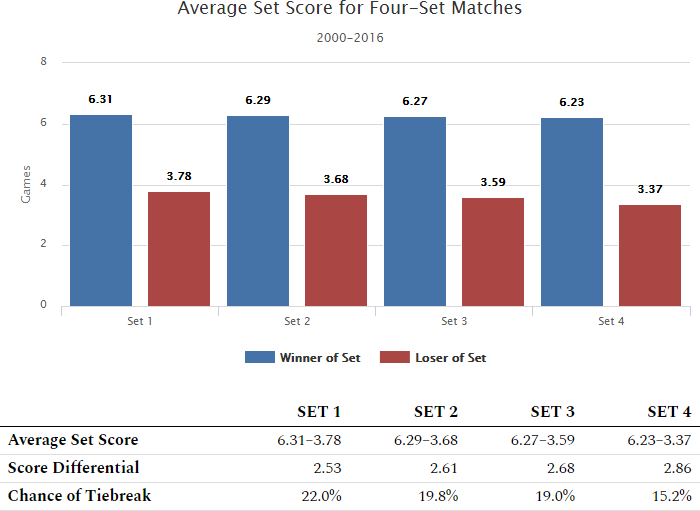
	Set 1	Set 2	Set 3	Set 4
Average Set Score	6.31–3.78	6.29–3.68	6.27–3.59	6.23–3.37
Score Differential	2.53	2.61	2.68	2.86
Chance of Tiebreak	22.0%	19.8%	19.0%	15.2%

Note:

The Average Set Score does not differentiate between who ultimately won or lost the match; it is a measure of the overall competitiveness of an average set.
There is a gradual decrease in competitiveness until the fourth set, which shows a greater increase in Score Differential and a greater decrease in tiebreaks as compared to the other sets.

Average Set Score for All Possible Four-Set Scorelines


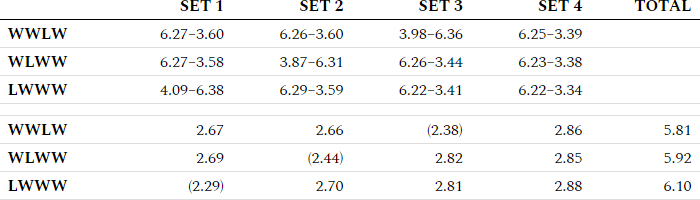
	Set 1	Set 2	Set 3	Set 4	Total
WWLW	6.27–3.60	6.26–3.60	3.98–6.36	6.25–3.39
WLWW	6.27–3.58	3.87–6.31	6.26–3.44	6.23–3.38
LWWW	4.09–6.38	6.29–3.59	6.22–3.41	6.22–3.34

WWLW	2.67	2.66	(2.38)	2.86	5.81
WLWW	2.69	(2.44)	2.82	2.85	5.92
LWWW	(2.29)	2.70	2.81	2.88	6.10

Note:

In each scoreline scenario, the winner of the match won each of his three sets more decisively than the only set won by the loser of the match.
The scenario most dominated by the winner of the match is the one where he loses the first set and goes on to win the next three. This is confirmed by the total Score Differential of 6.10 being the highest of all scenarios. As learned in the Analysis of Scorelines, this is also the most common of the four-set scenarios.

Five-Set Matches


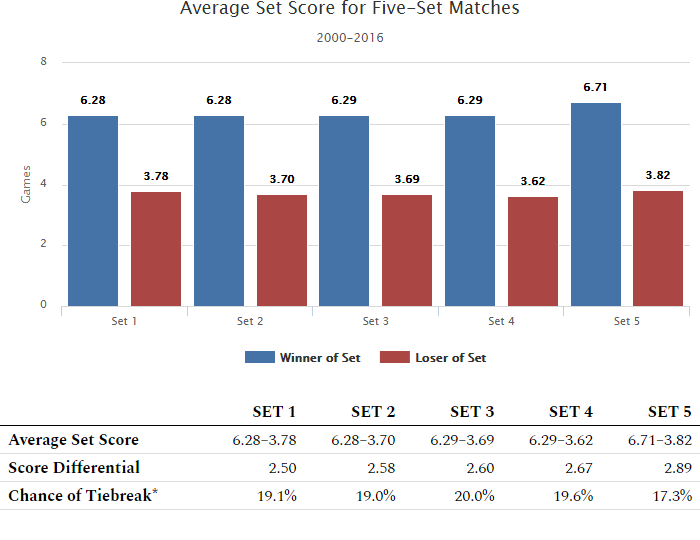
	Set 1	Set 2	Set 3	Set 4	Set 5
Average Set Score	6.28–3.78	6.28–3.70	6.29–3.69	6.29–3.62	6.71–3.82
Score Differential	2.50	2.58	2.60	2.67	2.89
Chance of Tiebreak*	19.1%	19.0%	20.0%	19.6%	17.3%

*Matches in majors, except for the U.S. Open, do not have tiebreaks in the fifth set. For purposes of this analysis only, a fifth set that extends past 6-6 is classified as a tiebreak.

Note:

The Average Set Score does not differentiate between who ultimately won or lost the match; it is a measure of the overall competitiveness of an average set.
As with three-set and four-set matches, there is a decrease in competitiveness as the match progresses. This is shown in the gradual increasing of the Score Differential. There is no clear pattern, however, regarding the odds of a tiebreak in each set.

Average Set Score for All Possible Five-Set Scorelines


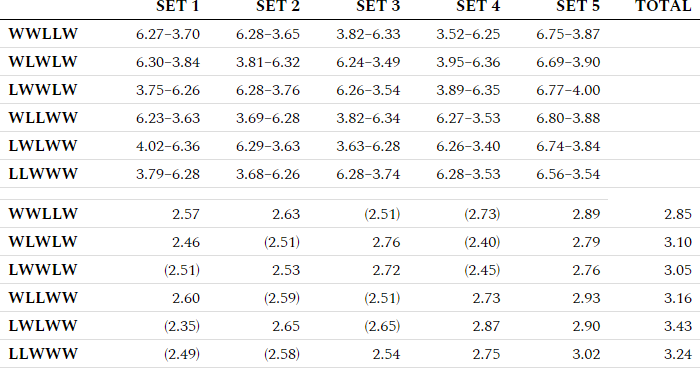
	Set 1	Set 2	Set 3	Set 4	Set 5	Total
WWLLW	6.27–3.70	6.28–3.65	3.82–6.33	3.52–6.25	6.75–3.87
WLWLW	6.30–3.84	3.81–6.32	6.24–3.49	3.95–6.36	6.69–3.90
LWWLW	3.75–6.26	6.28–3.76	6.26–3.54	3.89–6.35	6.77–4.00
WLLWW	6.23–3.63	3.69–6.28	3.82–6.34	6.27–3.53	6.80–3.88
LWLWW	4.02–6.36	6.29–3.63	3.63–6.28	6.26–3.40	6.74–3.84
LLWWW	3.79–6.28	3.68–6.26	6.28–3.74	6.28–3.53	6.56–3.54

WWLLW	2.57	2.63	(2.51)	(2.73)	2.89	2.85
WLWLW	2.46	(2.51)	2.76	(2.40)	2.79	3.10
LWWLW	(2.51)	2.53	2.72	(2.45)	2.76	3.05
WLLWW	2.60	(2.59)	(2.51)	2.73	2.93	3.16
LWLWW	(2.35)	2.65	(2.65)	2.87	2.90	3.43
LLWWW	(2.49)	(2.58)	2.54	2.75	3.02	3.24

Note:

The winner of the match won his sets more decisively as the match progressed with the fifth set being his best.
There are three scenarios where the winner of the match wins the final two sets; these are the most dominant victories and whose fifth sets are the most decisive.

Predictive Indicators

When the match is tied at two sets apiece, does a player's performance in the first four sets provide any indication of who will win the fifth set? That is, if one of the players has won more games than his opponent as the fifth set begins, does he have an historical edge in winning the match?


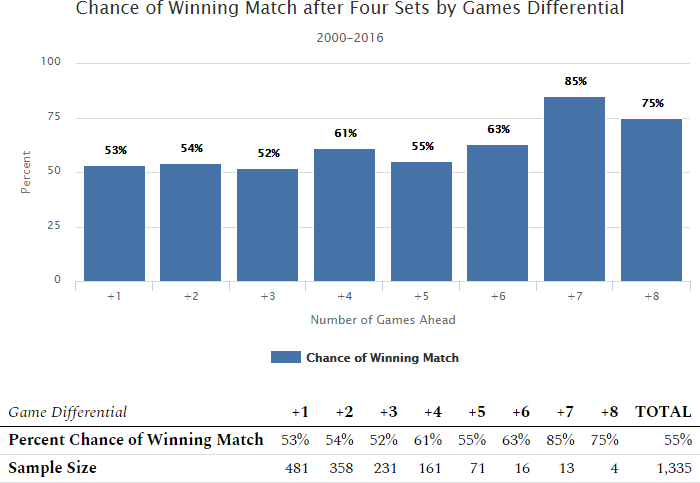
Game Differential	+1	+2	+3	+4	+5	+6	+7	+8	Total
Percent Chance of Winning Match	53%	54%	52%	61%	55%	63%	85%	75%	55%
Sample Size	481	358	231	161	71	16	13	4	1,335

Note:

If a player has won more games than his opponent after four sets, he goes on to win 55% of the matches; specific percentages per how many games ahead are indicated above. For example: If the scoreline after four sets is 6-2,4-6,6-1,3-6, one player leads in games 19-15. Historically, that player goes on to win the match 61% of the time.
In 15.1% of five-set matches, both players have won the same number of games after four sets thus offering no predictive information.
It is possible to be ahead by nine or ten games after four sets, but that has never happened in the years analyzed.

What about when the match is tied at one-set apiece? With a sample size of only two sets, is there any indication of who will win that match based on how many games each player has won?


	+1	+2	+3	+4	+5	Total
Percent Chance of Winning Match	54%	61%	60%	62%	76%	58%
Sample Size	1,067	639	257	106	17	2,086

Note:

If a player has won more games than his opponent after two sets, he goes on to win 58% of the matches; specific percentages per how many games ahead are indicated above.
In 24.6% of the matches tied at one set apiece, both players had won the same amount of games thus offering no predictive information.
Despite the smaller sample size, this is actually a more accurate indicator of the eventual winner of the match than the player who has won more games after four sets.

Tiebreak Distribution


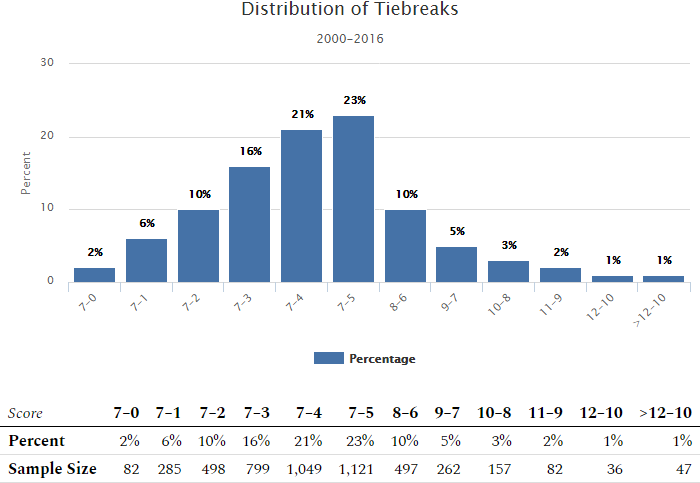
Score	7–0	7–1	7–2	7–3	7–4	7–5	8–6	9–7	10–8	11–9	12–10	>12–10
Percent	2%	6%	10%	16%	21%	23%	10%	5%	3%	2%	1%	1%
Sample Size	82	285	498	799	1,049	1,121	497	262	157	82	36	47

Note:

Out of a total of 4,915 tiebreaks, the average score was 7.48–4.32.

Acknowledgments

Most of the raw data used for analysis was gathered from the glorious repository of ATP match results compiled by Jeff Sackmann. Additional data from the ATP Web site filled in any gaps. A Microsoft Excel file is available for download if you wish to view the raw data that I compiled.

Sets	Winner of Set	Loser of Set
Three-Set Matches	6.22	3.30
Four-Set Matches	6.28	3.60
Five-Set Matches	6.37	3.72

Sets	Winner of Set	Loser of Set
Set 1	6.28	3.78
Set 2	6.28	3.70
Set 3	6.29	3.69
Set 4	6.29	3.62
Set 5	6.71	3.82

Score	Percentage
7-0	2%
7-1	6%
7-2	10%
7-3	16%
7-4	21%
7-5	23%
8-6	10%
9-7	5%
10-8	3%
11-9	2%
12-10	1%
>12-10	1%